Na zakładkach powyżej możesz wybrać odpowiedni dział sklepu.
Moonlight_A_ZS lampy wiszące, lampy wiszące led
Lampa wisząca czarna 7,5/12,3W SLED 2700K 630+996 lm >90+60° CRI≥ 97

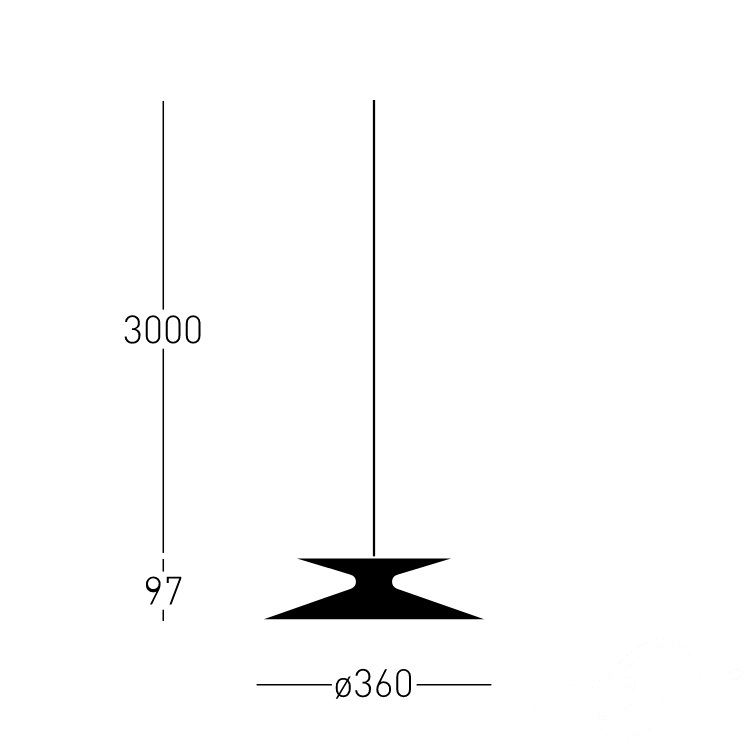
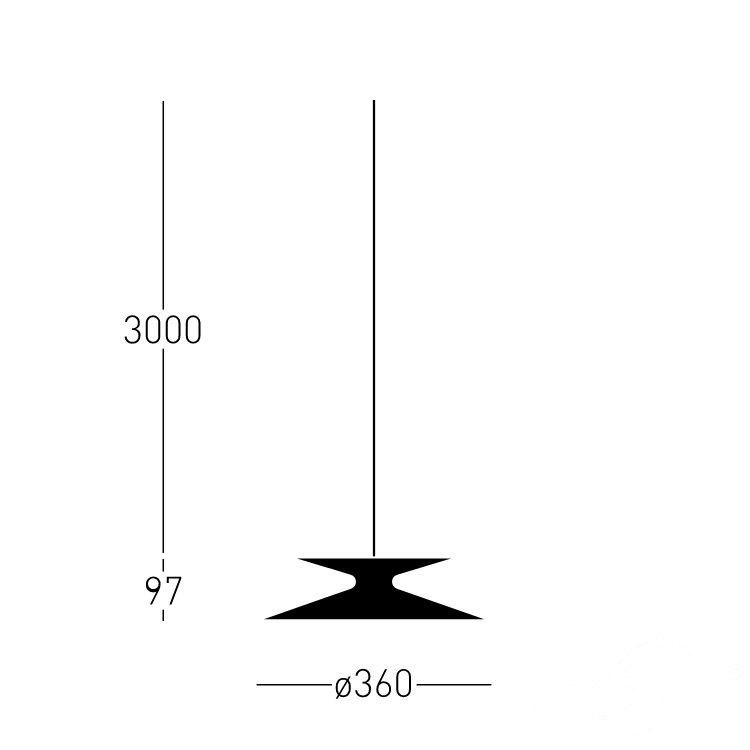
Moonlight to projekt Daniela Beckera - berlińskiego projektanta, tworzącego innowacyjne koncepcje i projekty oświetlenia, mebli, a także wystaw i produktów konsumenckich. Inspiracją do powstania oprawy Moonlight było zaćmienie księżyca. Od tego zjawiska pochodzi też nazwa oprawy. Skupione oświetlenie ze światłem pośrednim idealnie sprawdzi się w restauracjach, galeriach, klubach, hotelach, showroomach, pracowniach oraz we wnętrzach mieszkalnych. Moonlight ZS to oprawa przeznaczona do systemu Snap. Długość przewodu wynosi 3 metry.
Cena:
1 599 zł
| Styl: | Nowoczesne |
| Przeznaczenie: | Hotele,obiekty publiczne, Pokój, Holl/Korytarz, Biuro, Kuchnia / Jadalnia, Salon |
| Rodzaj trzonka żarówki: | zintegrowane |
| Źródło światła w zestawie: | Tak |
| Źródło światła: | LED - zintegrowany |
| Moc oprawy: | 7.5W LED, 12,5W LED |
| Barwa światła : | 2700K |
| Współczynnik oddawania barw (CRI): | CRI>97 |
| Strumień światła: | 630+996 lm |
| Kąt rozsyłu światła: | 60°, >90° |
| Napięcie zasilania: | 220-240V |
| Zasilacz: | 350 / 350 mA |
| Wysokość (cm): | 9,7 |
| Średnica (cm): | 36 |
| Producent: | CHORS |
| Długość przewodu / łańcucha (cm): | 300 cm |
| Stopień ochrony IP: | IP20 |
| Kolor producenta: | 002 Czarny (RAL 9005, drobna struktura) |
| Materiał: | aluminium |
| Funkcja ściemniania: | Opcjonalnie na zamówienie |
| Sprzedaż : | W sklepach firmowych KOMA na zamówienie |
| Uwagi: | Wymagany zasilacz |
| Klasa energetyczna EEL: | A++ szczegóły |
| Ilość punktów świetlnych: | 1 |
| Kolor pełna nazwa: | czarny |
| Montaż: | Wymagana baza SNAP |
Skonfiguruj produkt